To convert the regular expression (a + b)*abb from an NFA to a DFA using Thompson’s construction, we will follow these steps:
- Create an NFA for
(a + b)*abbusing Thompson’s construction. - Convert the NFA into a DFA using the subset construction method.
- Provide the transition table for the DFA.
- Draw the DFA diagram.
Step 1: NFA for (a + b)*abb
Breakdown of the Regular Expression:
(a + b)*: Any number ofaorb(including zero occurrences).abb: A fixed sequence ofafollowed by twobs.
NFA State Diagram:
States:
q0 -> initial state
q1 -> state for (a + b)*
q2 -> for the first 'a' of `abb`
q3 -> for the first 'b' of `abb`
q4 -> for the second 'b' of `abb` (final state)
Transitions:
- q0 --ε--> q1 (ε transition to begin the (a + b)*)
- q1 --a--> q1 (loop on `a` for (a + b)*)
- q1 --b--> q1 (loop on `b` for (a + b)*)
- q1 --a--> q2 (transition for the first 'a' in `abb`)
- q2 --b--> q3 (transition for the first 'b' in `abb`)
- q3 --b--> q4 (transition for the second 'b' in `abb`)
Final State: q4
The NFA accepts strings of any length from (a + b)* and ends with the substring abb.
Step 2: Convert NFA to DFA Using Subset Construction
We convert the NFA to DFA by determining the epsilon closures and forming new DFA states as combinations of NFA states.
Steps:
- Start with the epsilon closure of the start state (
q0), which includes{q0, q1}. - Calculate transitions for each input (
aandb) from this new DFA state by taking the union of all possible NFA states that can be reached from any state in the set. - Repeat this process for every new DFA state until all possible transitions are covered.
- Mark final states: A DFA state is a final state if it contains the NFA final state
q4.
Subset Construction Table (DFA Creation)
| DFA States | NFA States | On ‘a’ | On ‘b’ | Final? |
|---|---|---|---|---|
| A | {q0, q1} | {q1, q2} | {q1} | No |
| B | {q1, q2} | {q1, q2} | {q3} | No |
| C | {q1} | {q1, q2} | {q1} | No |
| D | {q3} | ∅ | {q4} | No |
| E | {q4} | ∅ | ∅ | Yes |
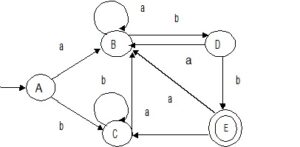
Step 3: DFA Transition Table
Here’s the transition table for the DFA created through subset construction:
| State | On ‘a’ | On ‘b’ | Is Final |
|---|---|---|---|
| A | B | C | No |
| B | B | D | No |
| C | B | C | No |
| D | – | E | No |
| E | – | – | Yes |
- A: Start state representing the NFA’s
{q0, q1}. - B: Represents NFA’s
{q1, q2}, which corresponds to reading anafrom(a + b)*or reaching the firstainabb. - C: Represents NFA’s
{q1}, looping through(a + b)*without matchingabb. - D: Represents reaching the first and second
bofabb. - E: The final state where
abbis fully matched.
Step 4: DFA State Diagram
Now, we can draw the DFA state diagram: