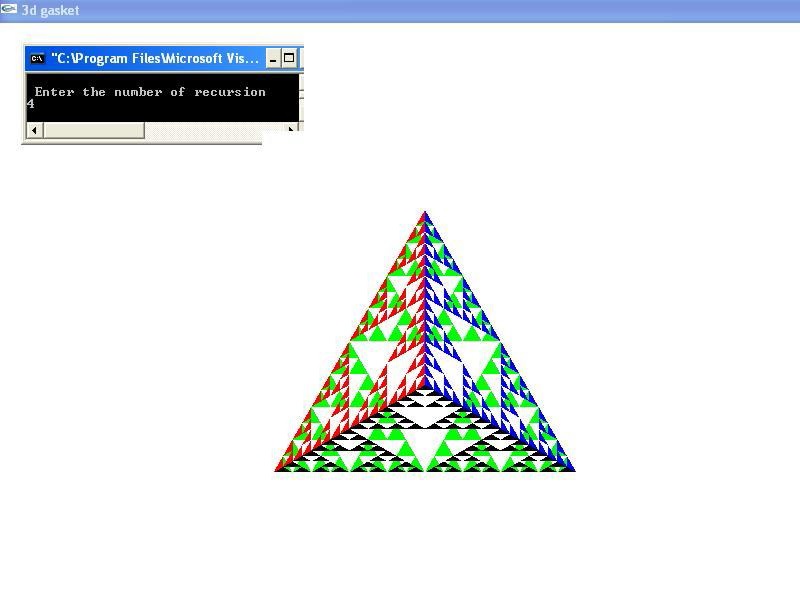
Algorithm:
Step 1: Specify the four vertices that form a tetrahedron
Step 2: Input the number of subdivisions n.
Step 3: Select any three vertices that form one of the triangular faces of the tetrahedron
Step 4: Find the mid-points of the edges that form the triangular face
Step 5: Subdivide the triangular face by drawing three triangles using the original vertices and the midpoints.
Step 6: Decrement n by one
Step 7: if n ≠ 0, then select each newly formed triangle and subdivide them recursively.
Step 8: if n ==0, select the next three set of original vertices that form the tetrahedron and repeat the steps 4 to 7.
Program: //Sierpinski Gasket
#include <stdio.h>
#include <GL/glut.h>
typedef float point[3];
/* initial tetrahedron */
point v[]={
{0.0, 0.0, 1.0}, {0.0, 0.9, -0.3}, {-0.8, -0.4, -0.3}, {0.8, -0.4, -0.3}
};
int n;
/* display one triangle using a line loop for wire frame, a single normal for constant shading, or three normals for interpolative shading */
void triangle( point a, point b, point c)
{
glBegin(GL_POLYGON);
glNormal3fv(a);
glVertex3fv(a);
glVertex3fv(b);
glVertex3fv(c);
glEnd();
}
/* triangle subdivision using vertex numbers right-hand rule applied to create outward pointing faces */
void divide_triangle(point a, point b, point c, int m)
{
point v1, v2, v3;
int j;
if(m>0)
{
for(j=0;j<3;j++)
{
v1[j] = (a[j] + b[j])/2;
v2[j] = (a[j] + c[j])/2;
v3[j] = (b[j] + c[j])/2;
}
divide_triangle(a, v1, v2, m-1);
divide_triangle(c, v2, v3, m-1);
divide_triangle(b, v3, v1, m-1);
}
else
triangle(a,b,c);
/*draw triangle at end of recursion */
}
void tetrahedron( int m)
{
/* Apply triangle subdivision to faces of tetrahedron */
glColor3f(1.0,0.0,0.0);
divide_triangle(v[0], v[1], v[2], m);
glColor3f(0.0,1.0,0.0);
divide_triangle(v[3], v[2], v[1], m);
glColor3f(0.0,0.0,1.0);
divide_triangle(v[0], v[3], v[1], m);
glColor3f(0.0,0.0,0.0);
divide_triangle(v[0], v[2], v[3], m);
}
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
tetrahedron(n);
glFlush();
}
void myReshape(int w, int h)
{
glViewport(0, 0, w, h);
(x,y,width,height) glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-2.0, 2.0, -2.0 *(GLfloat) h / (GLfloat) w, 2.0 * (GLfloat) h / (GLfloat) w, -10.0,10.0);
else
{
glOrtho(-2.0 * (GLfloat) w / (GLfloat) h, 2.0*(GLfloat)w/(GLfloat)h,-2.0,2.0,-10.0,10.0);
glMatrixMode(GL_MODELVIEW);
glutPostRedisplay();
}
}
int main(int argc, char **argv)
{
printf(" Enter the number of recursion: \n");
scanf("%d",&n);
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(500, 500);
glutCreateWindow("3D Gasket");
glutReshapeFunc(myReshape);
glutDisplayFunc(display); glEnable(GL_DEPTH_TEST);
glClearColor (1.0, 1.0, 1.0, 1.0);
glutMainLoop();
return 0;
}