Prim’s Algorithm:
Prim‟s algorithm finds the minimum spanning tree for a weighted connected graph G=(V,E) to get an acyclic subgraph with |V|-1 edges for which the sum of edge weights is the smallest. Consequently the algorithm constructs the minimum spanning tree as expanding sub-trees. The initial subtree in such a sequence consists of a single vertex selected arbitrarily from the set V of the graph‟s vertices. On each iteration, we expand the current tree in the greedy manner by simply attaching to it the nearest vertex not in that tree. The algorithm stops after all the graph‟s vertices have been included in the tree being constructed.
Complexity: The time efficiency of prim‟s algorithm will be in O(|E| log |V|).
#include<stdio.h>
#include<conio.h>
int a,b,u,v,n,i,j,ne=1;
int visited[10]={0},min,mincost=0,cost[10][10];
void main()
{
clrscr();
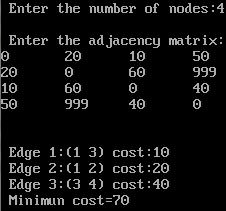
printf("\n Enter the number of nodes:");
scanf("%d",&n);
printf("\n Enter the adjacency matrix:\n");
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
scanf("%d",&cost[i][j]);
if(cost[i][j]==0)
cost[i][j]=999;
}
visited[1]=1;
printf("\n");
while(ne<n)
{
for(i=1,min=999;i<=n;i++)
for(j=1;j<=n;j++)
if(cost[i][j]<min)
if(visited[i]!=0)
{
min=cost[i][j];
a=u=i;
b=v=j;
}
if(visited[u]==0 || visited[v]==0)
{
printf("\n Edge %d:(%d %d) cost:%d",ne++,a,b,min);
mincost+=min;
visited[b]=1;
}
cost[a][b]=cost[b][a]=999;
}
printf("\n Minimun cost=%d",mincost);
getch();
}