Single Source Shortest Paths Problem:
For a given vertex called the source in a weighted connected graph, find the shortest paths to all its other vertices. Dijkstra‟s algorithm is the best known algorithm for the single source shortest paths problem. This algorithm is applicable to graphs with nonnegative weights only and finds the shortest paths to a graph‟s vertices in order of their distance from a given source. It finds the shortest path from the source to a vertex nearest to it, then to a second nearest, and so on. It is applicable to both undirected and directed graphs
Complexity: The Time efficiency for graphs represented by their weight matrix and the priority queue implemented as an unordered array and for graphs represented by their adjacency lists and the priority queue implemented as a min-heap, it is O(|E| log |V|).
#include<stdio.h>
#include<conio.h>
#define infinity 999
void dij(int n,int v,int cost[10][10],int dist[100])
{
int i,u,count,w,flag[10],min;
for(i=1;i<=n;i++)
flag[i]=0,dist[i]=cost[v][i];
count=2;
while(count<=n)
{
min=99;
for(w=1;w<=n;w++)
if(dist[w]<min && !flag[w])
min=dist[w],u=w;
flag[u]=1;
count++;
for(w=1;w<=n;w++)
if((dist[u]+cost[u][w]<dist[w]) && !flag[w])
dist[w]=dist[u]+cost[u][w];
}
}
void main()
{
int n,v,i,j,cost[10][10],dist[10];
clrscr();
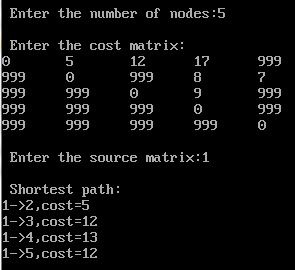
printf("\n Enter the number of nodes:");
scanf("%d",&n);
printf("\n Enter the cost matrix:\n");
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
scanf("%d",&cost[i][j]);
if(cost[i][j]==0)
cost[i][j]=infinity;
}
printf("\n Enter the source matrix:");
scanf("%d",&v);
dij(n,v,cost,dist);
printf("\n Shortest path:\n");
for(i=1;i<=n;i++)
if(i!=v)
printf("%d->%d,cost=%d\n",v,i,dist[i]);
getch();
}