Floyd’s Algorithm:
Floyd‟s algorithm is applicable to both directed and undirected graphs provided that they do not contain a cycle. It is convenient to record the lengths of shortest path in an n- by- n matrix D called the distance matrix. The element dij in the ith row and jth column of matrix indicates the shortest path from the ith vertex to jth vertex (1<=i, j<=n). The element in the ith row and jth column of the current matrix D(k-1) is replaced by the sum of elements in the same row i and kth column and in the same column j and the kth column if and only if the latter sum is smaller than its current value.
Complexity: The time efficiency of Floyd‟s algorithm is cubic i.e. Θ (n^3)
#include<stdio.h>
#include<conio.h>
int min(int,int);
void floyds(int p[10][10],int n)
{
int i,j,k;
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
p[i][j]=0;
else
p[i][j]=min(p[i][j],p[i][k]+p[k][j]);
}
int min(int a,int b)
{
if(a<b)
return(a);
else
return(b);
}
void main()
{
int p[10][10],w,n,e,u,v,i,j;
clrscr();
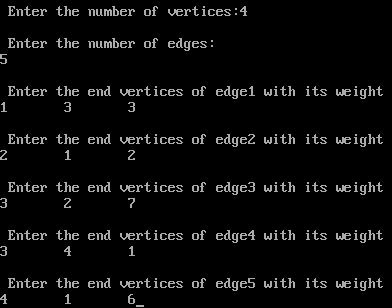
printf("\n Enter the number of vertices:");
scanf("%d",&n);
printf("\n Enter the number of edges:\n");
scanf("%d",&e);
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
p[i][j]=999;
}
for(i=1;i<=e;i++)
{
printf("\n Enter the end vertices of edge%d with its weight \n",i);
scanf("%d%d%d",&u,&v,&w);
p[u][v]=w;
}
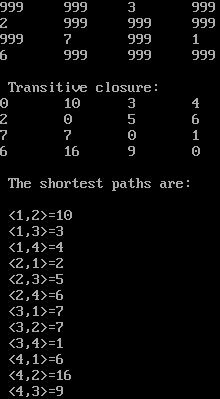
printf("\n Matrix of input data:\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%d \t",p[i][j]);
printf("\n");
}
floyds(p,n);
printf("\n Transitive closure:\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%d \t",p[i][j]);
printf("\n");
}
printf("\n The shortest paths are:\n");
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(i!=j)
printf("\n <%d,%d>=%d",i,j,p[i][j]);
}
getch();
}