N Queen’s problem: The n-queens problem consists of placing n queens on an n x n checker board in such a way that they do not threaten each other, according to the rules of the game of chess. Every queen on a checker square can reach the other squares that are located on the same horizontal, vertical, and diagonal line.
So there can be at most one queen at each horizontal line, at most one queen at each vertical line, and at most one queen at each of the 4n-2 diagonal lines. Furthermore, since we want to place as many queens as possible, namely exactly n queens, there must be exactly one queen at each horizontal line and at each vertical line.
The concept behind backtracking algorithm which is used to solve this problem is to successively place the queens in columns. When it is impossible to place a queen in a column (it is on the same diagonal, row, or column as another token), the algorithm backtracks and adjusts a preceding queen
Complexity: The power of the set of all possible solutions of the n queen‟s problem is n! and the bounding function takes a linear amount of time to calculate, therefore the running time of the n queens problem is O (n!).
#include<stdio.h>
#include<conio.h>
#include<math.h>
int a[30],count=0;
int place(int pos)
{
int i;
for(i=1;i<pos;i++)
{
if((a[i]==a[pos])||((abs(a[i]-a[pos])==abs(i-pos))))
return 0;
}
return 1;
}
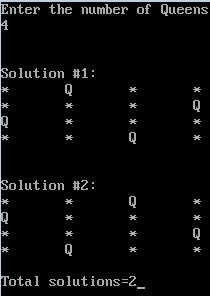
void print_sol(int n)
{
int i,j;
count++;
printf("\n\nSolution #%d:\n",count);
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(a[i]==j) printf("Q\t");
else
printf("*\t");
}
printf("\n");
}
}
void queen(int n)
{
int k=1;
a[k]=0;
while(k!=0)
{
a[k]=a[k]+1;
while((a[k]<=n)&&!place(k))
a[k]++;
if(a[k]<=n)
{
if(k==n)
print_sol(n);
else
{
k++;
a[k]=0;
}
}
else
k--;
}
}
void main()
{
int i,n;
clrscr();
printf("Enter the number of Queens\n");
scanf("%d",&n);
queen(n);
printf("\nTotal solutions=%d",count);
getch();
}