Topological Ordering:
This method is based on decrease and conquer technique a vertex with no incoming edges is selected and deleted along with no incoming edges is selected and deleted along with the outgoing edges. If there are several vertices with no incoming edges arbitrarily a vertex is selected. The order in which the vertices are visited and deleted one by one results in topological sorting.
1) Find the vertices whose indegree is zero and place them on the stack
2) Pop a vertex u and it is the task to be done
3) Add the vertex u to the solution vector
4) Find the vertices v adjacent to vertex u. The vertices v represents the jobs which depend on job u
5) Decrement indegree[v] gives the number of depended jobs of v are reduced by one
#include<stdio.h>
#include<conio.h>
int a[10][10],n,indegre[10];
void find_indegre()
{
int j,i,sum;
for(j=0;j<n;j++)
{
sum=0;
for(i=0;i<n;i++)
sum+=a[i][j];
indegre[j]=sum;
}
}
void topology()
{
int i,u,v,t[10],s[10],top=-1,k=0;
find_indegre();
for(i=0;i<n;i++)
{
if(indegre[i]==0)
s[++top]=i;
}
while(top!=-1)
{
u=s[top--];
t[k++]=u;
for(v=0;v<n;v++)
{
if(a[u][v]==1)
{
indegre[v]--;
if(indegre[v]==0)
s[++top]=v;
}
}
}
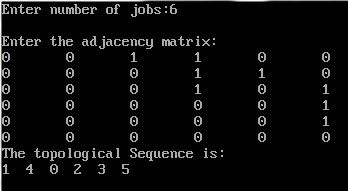
printf("The topological Sequence is:\n");
for(i=0;i<n;i++)
printf("%d ",t[i]);
}
void main()
{
int i,j;
clrscr();
printf("Enter number of jobs:");
scanf("%d",&n);
printf("\nEnter the adjacency matrix:\n");
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
scanf("%d",&a[i][j]);
}
topology();
getch();
}