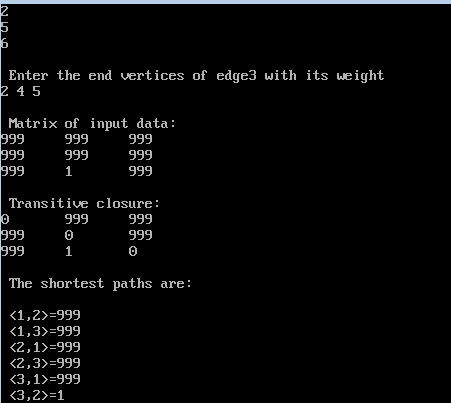
Objective: C program to find all pairs shortest path using Floyd’s algorithm
Concept: Floyd’s algorithm is applicable to both directed and undirected graphs provided that they do not contain a cycle. It is convenient to record the lengths of shortest path in an n- by- n matrix D called the distance matrix. The element dij in the ith row and jth column of matrix indicates the shortest path from the ith vertex to jth vertex (1<=i, j<=n). The element in the ith row and jth column of the current matrix D(k-1) is replaced by the sum of elements in the same row i and kth column and in the same column j and the kth column if and only if the latter sum is smaller than its current value.
Algorithm Floyd(W[1..n,1..n])
//Implements Floyd’s algorithm for the all-pairs shortest paths problem
//Input: The weight matrix W of a graph
//Output: The distance matrix of shortest paths length
{
D ← W
for k←1 to n do
{
for i ← 1 to n do
{
for j ← 1 to n do
{
D[i,j] ← min (D[i, j], D[i, k]+D[k, j] )
}
}
}
return D
}
#include<stdio.h>
#include<conio.h>
void floyd(int[10][10],int);
int min(int,int);
void main()
{
int n,a[10][10],i,j;
printf("Enter the no.of nodes : ");
scanf("%d",&n);
printf("\nEnter the cost adjacency matrix\n");
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&a[i][j]);
floyd(a,n); getch();
}
void floyd(int a[10][10],int n)
{
int d[10][10],i,j,k;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
d[i][j]=a[i][j];
}
for(k=1;k<=n;k++)
{
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
}
}
printf("\nThe distance matrix is\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
printf("%d\t",d[i][j]);
}
printf("\n");
}
}
int min (int a,int b)
{
if(a<b)
return a;
else
return b;
}