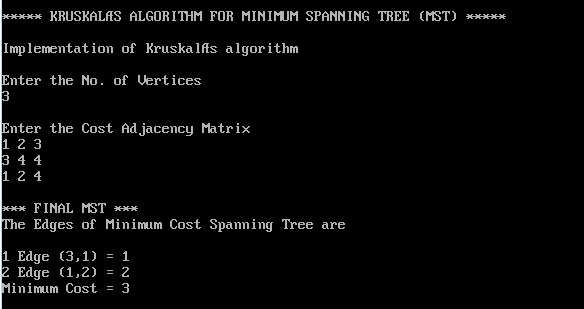
Objective: C program to find the minimum spanning tree to design Kruskal’s algorithm using greedy method
Time Complexities: The computing time is O(|E| log |E|) where E is the edge set of graph G.
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
int i,j,k,a,b,u,v,n,ne=1;
int min,mincost=0,cost[9][9],parent[9];
int find(int);
int uni(int,int);
void main()
{
clrscr();
printf(“\n***** KRUSKAL’S ALGORITHM FOR MINIMUM SPANNING TREE (MST) *****\n”);
printf(“\nImplementation of Kruskal’s algorithm\n”);
printf(“\nEnter the No. of Vertices\n”);
scanf(“%d”,&n); printf(“\nEnter the Cost Adjacency Matrix\n”);
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
scanf(“%d”,&cost*i+*j+);
if(cost[i][j]==0)
cost[i][j]=999;
}
}
printf(“\n*** FINAL MST ***”);
printf(“\nThe Edges of Minimum Cost Spanning Tree are\n”);
while(ne<n)
{
for(i=1,min=999;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(cost[i][j]<min)
{
min=cost[i][j];
a=u=i;
b=v=j;
}
}
}
u=find(u);
v=find(v);
if(uni(u,v))
{
printf(“\n%d Edge (%d,%d) = %d”,ne++,a,b,min);
mincost +=min;
}
cost[a][b]=cost[b][a]=999;
}
printf(“\nMinimum Cost = %d\n”,mincost);
getch();
}
int find(int i)
{
while(parent[i]) i=parent[i];
return i;
}
int uni(int i,int j)
{
if(i!=j)
{
parent[j]=i;
return 1;
}
return 0;
}