For every regular language there is a finite state automaton (FSA) that accepts the language. The number of states in such an FSA are counted and that count is used as the pumping length p. For a string of length at least p, let s0 be the start state and let s1, …, sp be the sequence of the next p states visited as the string is emitted. Because the FSA has only p states, within this sequence of p + 1 visited states there must be at least one state that is repeated. Write S for such a state. The transitions that take the machine from the first encounter of state S to the second encounter of state S match some string. This string is called y in the lemma, and since the machine will match a string without the y portion, or the string y can be repeated any number of times, the conditions of the lemma are satisfied.
For example, the following image shows an FSA.
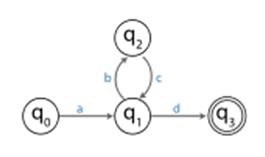
The FSA accepts the string: abcd. Since this string has a length which is at least as large as the number of states, which is four, the pigeonhole principle indicates that there must be at least one repeated state among the start state and the next four visited states. In this example, only q1 is a repeated state. Since the substringbc takes the machine through transitions that start at state q1 and end at state q1, that portion could be repeated and the FSA would still accept, giving the stringabcbcd. Alternatively, the bc portion could be removed and the FSA would still accept giving the string ad. In terms of the pumping lemma, the string abcd is broken into an x portion a, a y portion bc and a z portion d.
